Пятый постулат Евклида
Попытка доказательства аксиомы о параллельных прямых.
Пятый постулат геометрии Евклида гласит:
Если две прямые, лежащие в одной плоскости, пересечены третьей и если сумма внутренних односторонних углов меньше двух прямых, то эти прямые пересекутся с той стороны, где это имеет место.
Николай Иванович Лобачевский предположил, что данное утверждение может быть и неверным, т.е. что прямые могут и не пересечься. Попытки найти противоречие в этом предположении, сделанные Лобачевским, результатов не дали, так было положено начало первой геометрии, отличной от геометрии Евклида, называемой ныне геометрией Лобачевского.
Рассмотрим ключевые моменты геометрии Лобачевского, что позволит нам “договорится о терминах” и на этой основе подойти к основной задаче публикации.
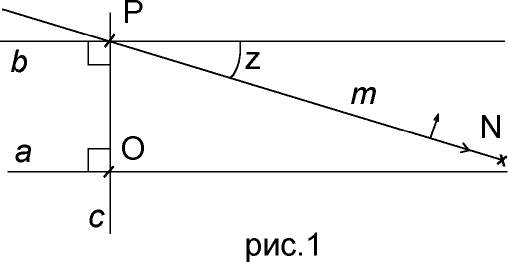
Итак, имеем две прямые
a и b лежащие в одной плоскости, пересеченные третьей прямой c (рис. 1). Углы при точках пересечения O и P данных прямых равны 90 градусам. Соответственно, сумма внутренних односторонних углов равна 180 градусам. Абсолютная геометрия, т.е. геометрия, не использующая пятый постулат Евклида в своих доказательствах, утверждает, что такие прямые не пересекутся.
Теперь построим прямую
m проходящую через точку P и образующую с прямой b некоторый, сколь угодно малый, угол z. Таким образом мы получили две прямые a и m, пересеченные третьей прямой c, причем сумма одной из пар внутренних односторонних углов меньше 180 градусов на величину z. Лобачевский допустил, что существует некоторая величина z такая, что прямая m не пересечет прямую a, будучи как угодно далеко продленной.Действительно, если поставить воображаемый эксперимент по продлению прямой
m в направлении сближения с прямой a, можно заметить что, как только “отслеживаемая точка” N, движущаяся в воображении по прямой m, приблизиться к прямой a, мы всегда можем уменьшить величину угла z, и продолжить движение не пересекая прямую a. И так “до бесконечности”. Хотя это довольно профанирующий способ описания геометрии Лобачевского, причем только одного из ее ключевых моментов, но он позволяет несколько примирить сознание со столь не естественным для восприятия утверждением о том, что при таком построении прямые могут не пересечься.Приведенный выше способ апеллирует к невозможности верифицировать, или установить, момент пересечения прямых в конкретной точке, но Лобачевский исходил из несколько других предположений. А именно из того, что пятый постулат Евклида ни откуда не следует и является лишь нашим “ощущением” того, как должны вести себя прямые в случае пятого постулата. Соответственно Лобачевский не пытался объяснить, как прямые не пересекаются, а выдвинул утверждение, в ранге аксиомы, что существуют такие прямые, которые не пересекаются.
Однако весь опыт человечества подсказывает, что должны существовать и пересекающиеся прямые, упомянутые в пятом постулате Евклида. Соответственно должен существовать “пограничный” случай, когда прямая
m из не пересекающей прямую a, превращается в пересекающую данную прямую.Если поворачивать прямую
m по часовой стрелке вокруг точки P (рис. 2), угол z будет возрастать, что неминуемо приведет к такой ситуации, когда прямая m “в последний раз” не пересечет прямую a.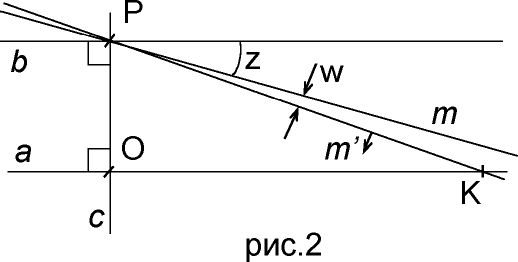
Теперь если довернуть прямую
m на сколь угодно малую величину w, прямая m перейдет в прямую m’. Эта прямая пересечет прямую a, в некоторой точке K.Таким образом, имеется прямая
L, являющаяся “пограничной” прямой, отделяющей прямые, которые пересекут прямую a, от прямых которые не пересекут данную прямую (рис. 3). Сама прямая L не пересекает прямую a.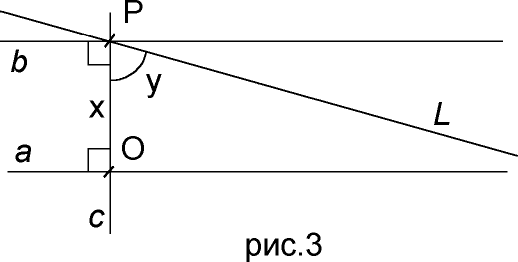
Не трудно заметить, что угол
y зависит от длины отрезка OP - чем отрезок короче, тем больше должен быть угол и наоборот. Обозначив длину отрезка OP через x, Лобачевский вводит специальную функцию для угла y = П(х), определяющую зависимость угла от длины отрезка, а сам угол называет “углом параллельности” отрезка данной длины. При изменении x от 0 до ∞, угол y стремится от 90 к 0 градусов.Здесь стоит обратить внимание, что в геометрии Лобачевского, связываются два таких параметра как угол и длина, что влечет за собой абсолютизацию длины, так как величина угла изменяется в определенных пределах. Если взять угол данной величины, то ему будет соответствовать длина определенного размера. Считается, что длина, при которой будет заметно сказываться отличие геометрии Лобачевского от геометрии Евклида, должна быть вселенских размеров, размеры же порядка, например, галактики в геометрии Лобачевского считаются малыми.
Так выглядят основные тезисы геометрии Лобачевского, теперь можно перейти к главной задаче публикации. Начнем с доказательства достаточно очевидного, как может показаться, утверждения, что не освобождает его от необходимости быть доказанным. Тем более данное утверждение является базисным для всей работы. Для доказательства будем пользоваться аксиоматикой Гильберта, признанной непротиворечивой системой аксиом, полностью соответствующей геометрии Евклида. Используем две аксиомы:
G1. Для любых двух точек существует прямая, проходящая через каждую из этих двух точек.
G2. Для двух различных точек существует не более одной прямой, проходящей через каждую из этих двух точек.
Назовем утверждение как,
Теорема о расположении двух пересекающихся прямых.
Прямая, пересеченная другой прямой, делится пересекающей прямой на две части полностью лежащие по разные стороны от пересекающей прямой. Точка пересечения не входит ни в одну из частей. (Возможно, формулировка требует коррекции, но идея, как кажется, представляется достаточно ясной)
Предположим, что это не так. Тогда мы можем предложить два варианта расположения прямых.
Вариант
1.Хотя бы одна из частей пересеченной прямой лежит как по одну, так и по другую сторону от пересекающей прямой.
Итак, имеется прямая
a, и пересекающая ее в точке D, прямая b (рис 4).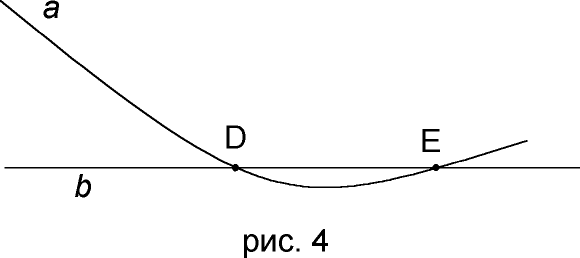
Допустим, что часть прямой
а лежащая справа (по рисунку 4) от точки пересечения D, лежит как с одной, так и с другой стороны от пересекающей прямой b. Тогда данная часть прямой a должна пересекаться с прямой b в некоторой точке E. Это в свою очередь означает, что через две точки проведено больше одной прямой, что противоречит аксиоме G2. Следовательно, такое расположение прямых невозможно.
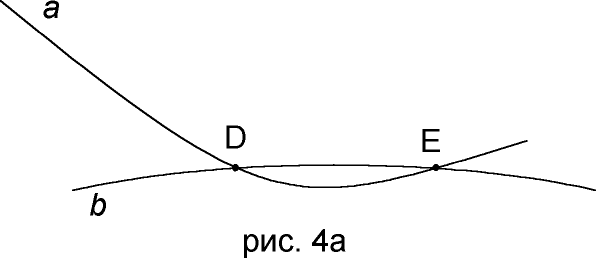
Заметим, что утверждение остается справедливым для прямых любого вида (рис 4
a).Вариант 2.
Две прямые лишь касаются в одной точкой. Тогда имеется прямая
a и прямая b которые, сближаясь, достигают друг друга в некоторой точке D, а затем снова расходятся друг от друга (рис 5).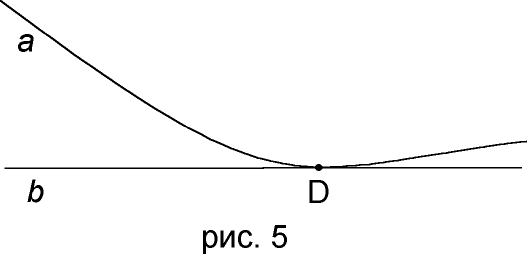
Теперь возьмем на прямой
a точку С, лежащую слева от точки D (рис 5a) и точку Е, лежащую на прямой b справа от точки D (рис 5a).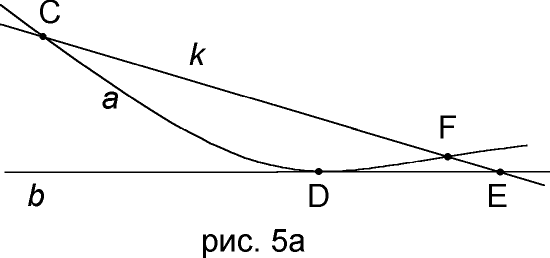
Проведем через точки
C и E прямую k. Мы можем это сделать в соответствии с аксиомой G1. Тогда для прямой k возможны два варианта расположения относительно точки D.Первый вариант, когда прямая
k проходит выше точки D (рис 5a), что влечет за собой неминуемое пересечение с прямой a, в некоторой точке F. Т.е. через две точки C и F проходит две прямые, что противоречит аксиоме G2.Второй вариант, когда прямая
k проходит ниже точки D (рис 5b). Этот вариант приводит к схожей с предыдущей ситуации, но в данном случае прямая k дважды пересекает прямую b, а именно в точках S и E, т.е. через две точки проходит две прямые, что также невозможно по аксиоме G2.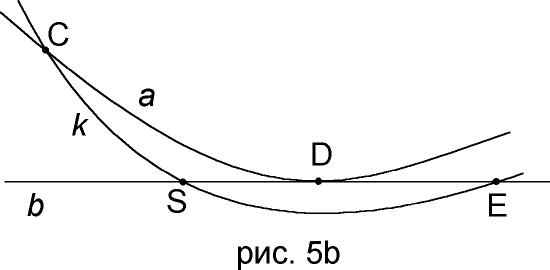
Опять стоит обратить внимание, что доказанное справедливо для прямых любого вида.
Осталось произнести знаменитое евклидово: “Что и требовалось доказать”.
Теорема о параллельных прямых
.Рассмотрим еще раз зависимость угла параллельности и расстояния между параллельными прямыми в геометрии Лобачевского.
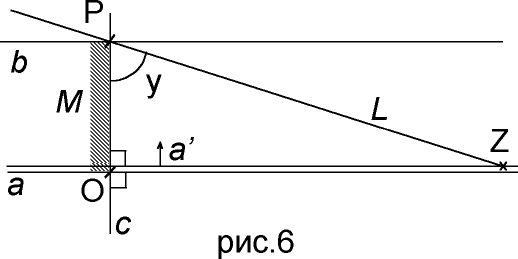
Как следует из геометрии Лобачевского, каждому данному углу параллельности
y найдется соответствующее расстояние OP, при котором прямая a не пересечется с прямой L (рис 6). При любом изменении угла параллельности y изменяется и расстояние OP. Соответственно верно и обратное при изменении расстояния OP должен изменятся угол параллельности y. Если же угол y оставить прежним, но сократить расстояние OP на сколь угодно малую величину, тогда прямая a перейдет в прямую a’, пересекающуюся с прямой L в некоторой точке Z. Отсюда можно заключить, что существует некоторая область M, ограниченная снизу (по рисунку) прямой a и сверху прямой b. Внутри данной области располагаются прямые, перпендикулярные прямой c и, что существенно, все эти прямые пересекаются с прямой L. Для большей строгости заметим, что существует также область симметричная области M, относительно прямой b (хотя данное замечание не существенно для доказательства). Как следует из геометрии Лобачевского, прямая a не входит в область M, т.е. не пересекается прямой L.Теперь если применить выше доказанную теорему о расположении пересекающихся прямых, к прямым находящимся внутри области
M и прямой L, можно заметить, что любая прямая перпендикулярная прямой c и находящаяся в области M делит прямую L на две части, лежащие как выше, так и ниже (по рисунку) от пересекающей прямой. Это же утверждение справедливо и для крайне нижней (по рисунку) прямой, перпендикулярной прямой c, и находящейся в области M. Соответственно, одна из двух частей прямой L, образовавшихся вследствие пересечения такой прямой, должна располагаться ниже (по рисунку) пересекающей ее прямой. Но так как прямая пересекающая прямую L, была крайне нижней из области M, то прямая L, должна пересечь и прямую a, находящуюся ниже области M. Данное доказательство справедливо для любого угла параллельности y и для любого расстояния OP.Отсюда следует, что утверждение противоположное утверждению из пятого постулата Евклида, что существует некоторый угол меньший суммы двух прямых углов, при котором прямые пятого постулата не пересекутся не верно.
Что и требовалось доказать.
17 декабря 2005
e-mail: kos1@yandex.ru